18. 拉普拉斯变换
如果用拉普拉斯变换，在控制电路的设计中必要的微分・积分等复杂运算可以用简单的乘除法等代数运算替换。拉普拉斯变换的定义如下。
对t≧0时被定义的时间函数f（t），在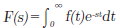
中被定义的F（s）叫做f（t）的拉普拉斯变换。右边表示了基本函数的拉普拉斯变换。
| 函数名 | 时间函数f(t) | 拉普拉斯变换 F(s) |
|---|---|---|
| 单位冲击函数 |
δ(t) |
1 |
|
单位阶跃函数 |
1 |
|
|
单位斜坡函数 |
t |
|
|
|
|
|
指数函数 |
|
|
|
正弦函数 |
sin ωt |
|
|
余弦函数 |
cos ωt |
|
|
双曲线正弦（塞恩）函数 |
sinh ωt |
|
|
双曲线余弦（口塞恩）函数 |
cosh ωt |
|
sinc函数 |
|
|
|
其他函数 |
|
|
|
|
|
|
|
|
t sin ωt |
|
|
t cos ωt |
|